Automatic Euler-Lagrange Transformation of Nonlinear Progressive Waves in Water of Uniform Depth
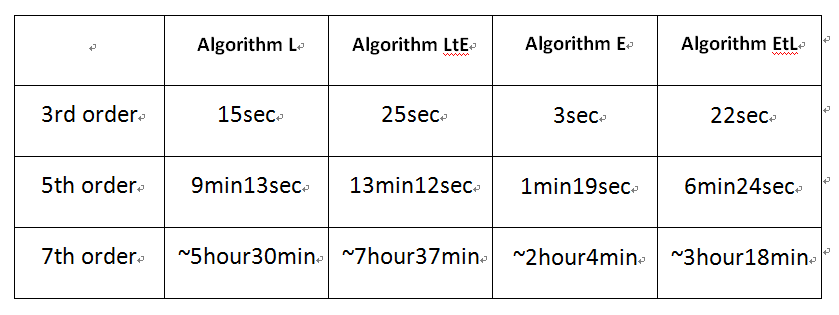
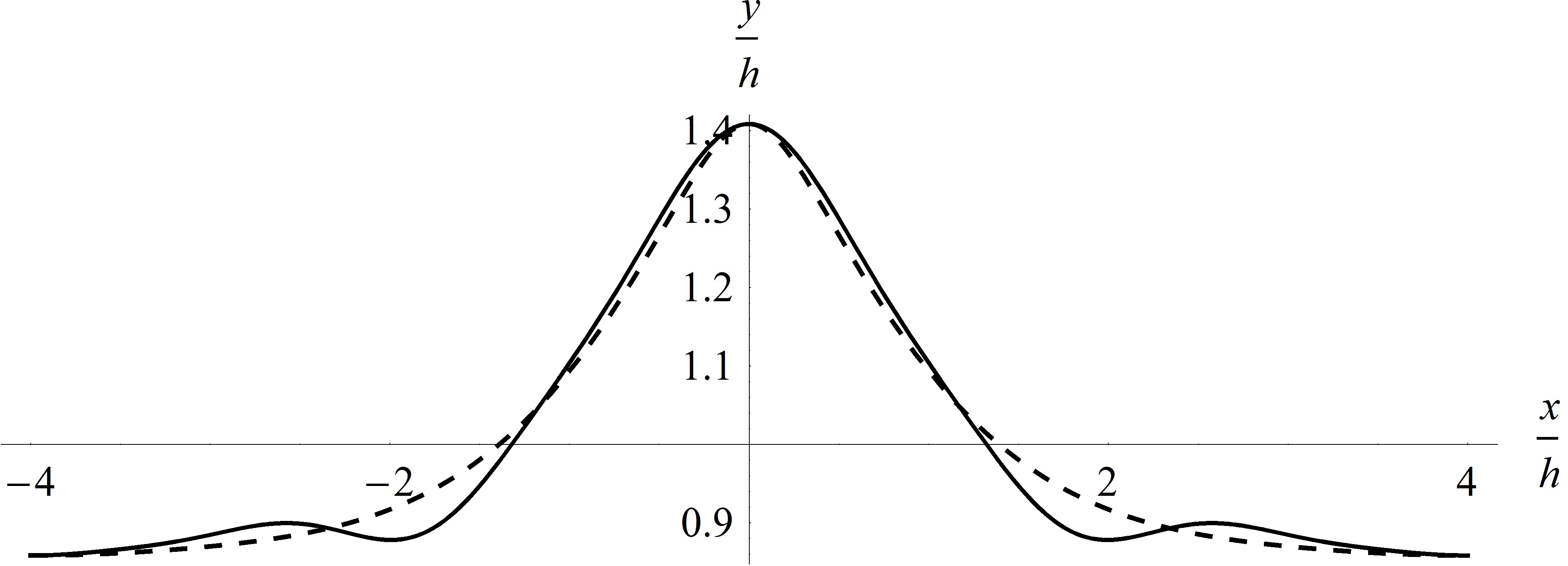
In this study, we provide a technical note for the implementation of a symbolic Euler-Lagrange transformation on nonlinear progressive water waves. By the implementation, the solution of nonlinear steady waves in the Eulerian description can be obtained and then transformed to the corresponding solution in the Lagrangian description automatically. We consider four closure conditions in a single symbolic implementation to derive both the Eulerian and Lagrangian solutions. In order to accomplish an automatically symbolic computation, we propose trigonometry-polynomial transformations to convert the hierarchical system of differential equations of different orders into a system of algebraic ones. During the symbolic computation, the solutions of a user-prescribed order can be automatically obtained via multiple loops. For example, the fifth-order Euler-Lagrange solutions can be obtained within 7 minutes by a usual PC system. In addition, the seventh-order solutions in the Eulerian and Lagrangian frameworks are firstly obtained by the present code. (Tsai et al., 2015)
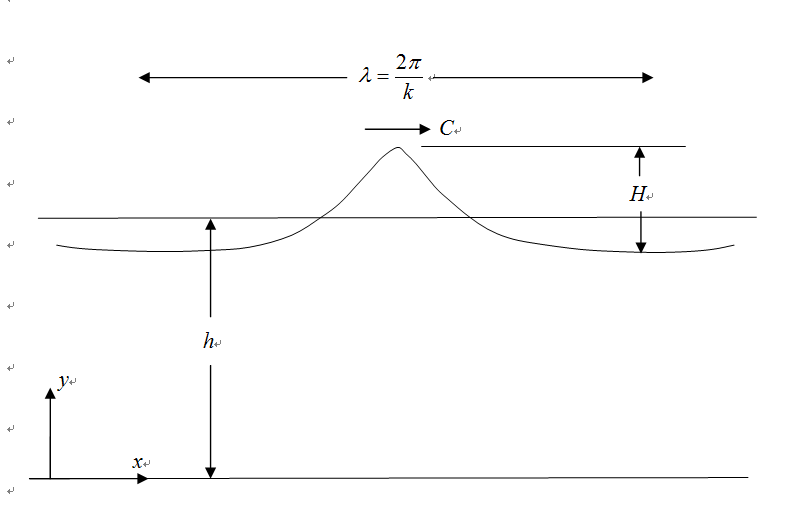
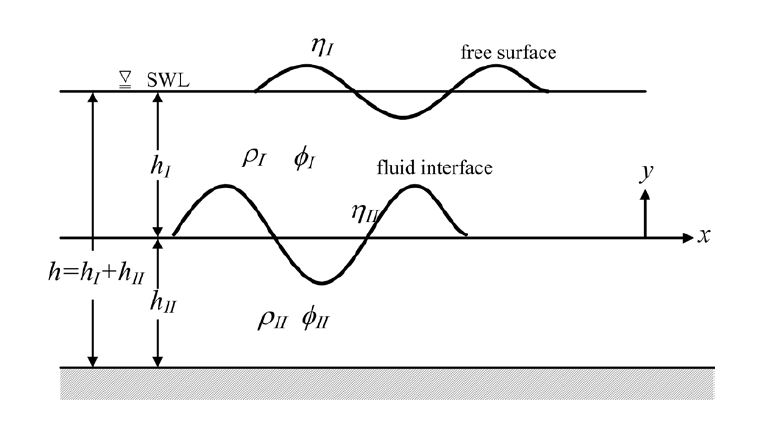
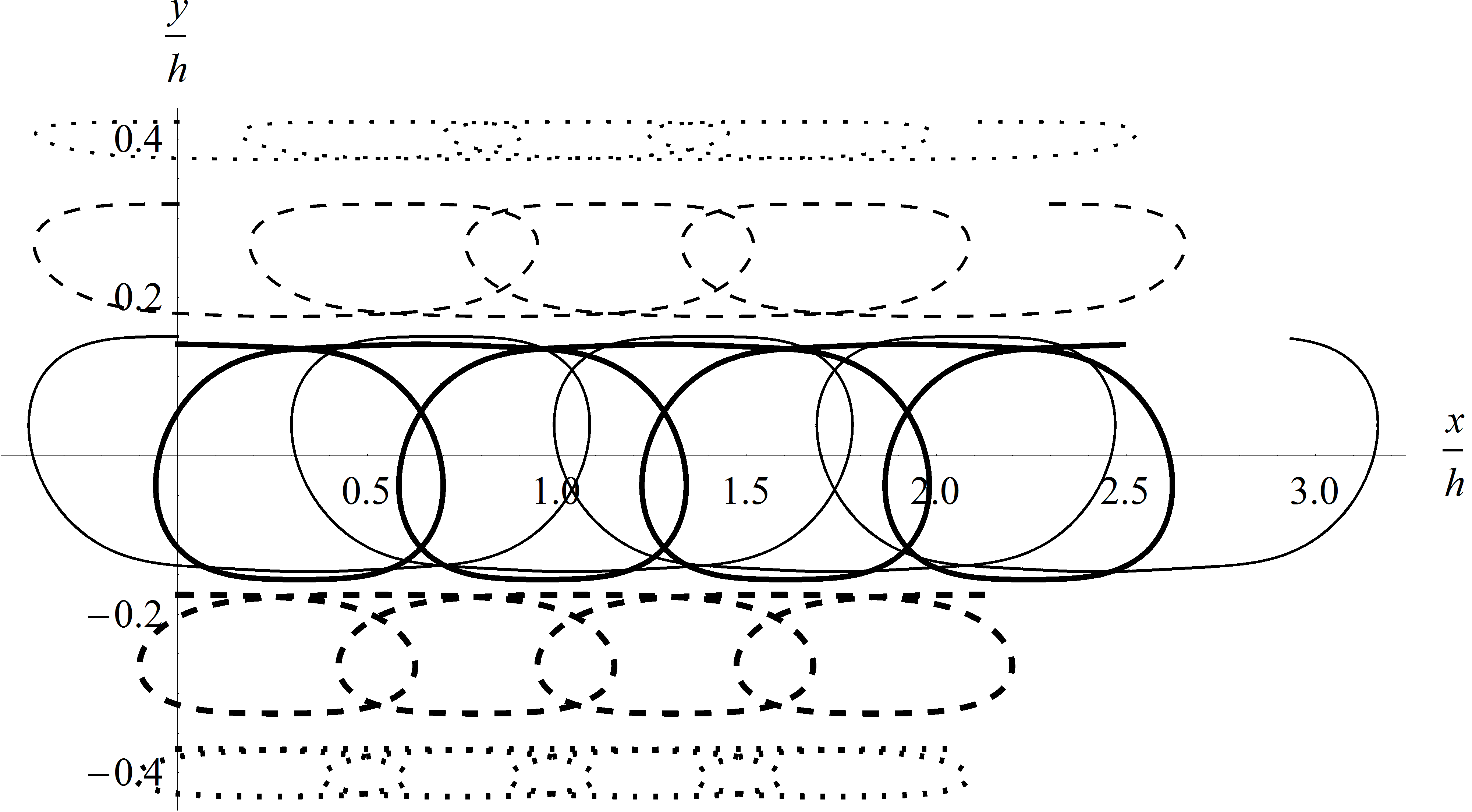
Lagrangian approach to interfacial water waves with free surface
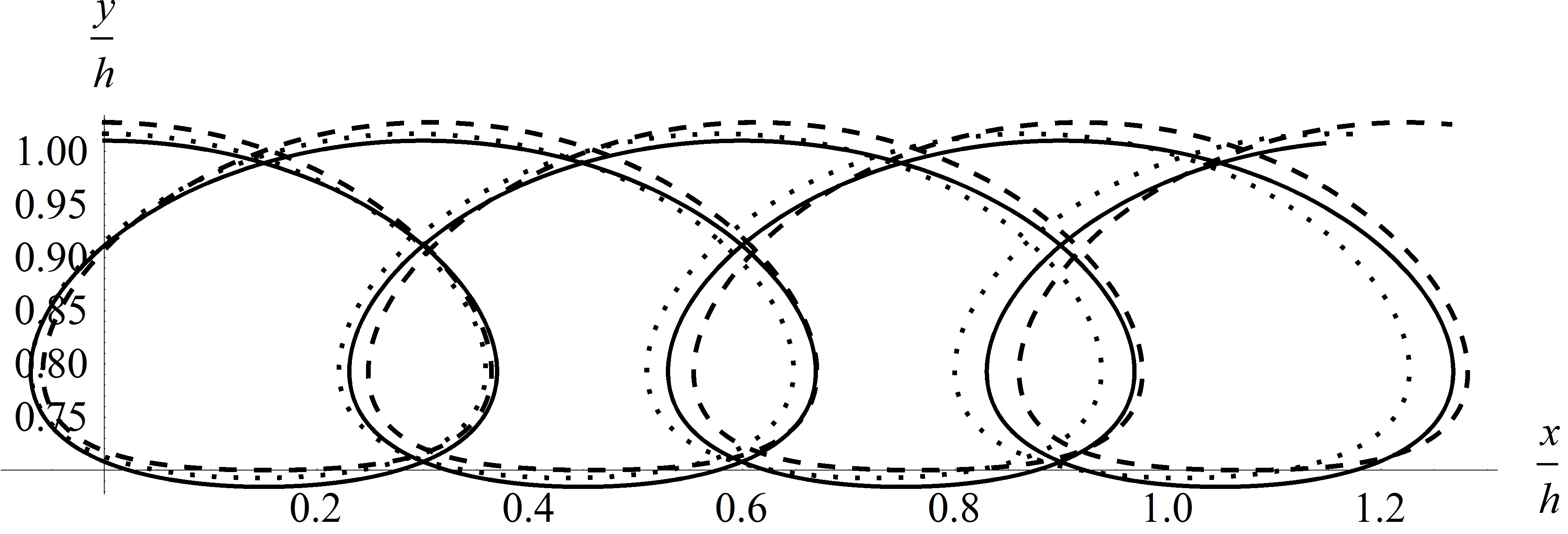
This is a theoretical study on the interfacial water waves with a free surface in a two-layer system, where the lower fluid is taken to be heavier than the upper one. Lagrangian matching conditions are introduced for the physical fields separated by the interface. And a perturbation analysis is carried out to the third order to find the particle trajectory in the Lagrangian description. Observing the derived solution, a symbolic computation is introduced for obtaining the fifth order solution. The Lagrangian drifts, wave frequency, and set-up are also given as part of the solutions. Discontinuities across the interface are found for all of these physical quantities. A generalized set-up effect is found that the Lagrangian mean levels come near to both of the free surface and internal interface.

Reference
Chia-Cheng Tsai, Yang-Yih Chen and Hung-Chu Hsu (2015, Aug). Automatic Euler-Lagrange transformation of nonlinear progressive waves in water of uniform depth. Coastal Engineering Journal, 57(3), 1550011.
Software